scipy.stats.ppcc_max¶

scipy.stats.ppcc_max(x, brack=(0.0, 1.0), dist='tukeylambda')[源代码]¶

计算使PPCC最大化的形状参数。

概率图相关系数(PPCC)图可用于确定单参数分布族的最佳形状参数。 ppcc_max 将使给定数据的概率图相关系数最大化的形状参数返回到单参数分布族。

参数

xarray_like: 输入数组。
brack元组，可选: 三(a，b，c)式中(a<b<c)。如果括号由两个数字(a，c)组成，则假定它们是下坡括号搜索的起始间隔(请参见 scipy.optimize.brent )。
dist字符串或统计信息。分布实例，可选: 分发或分发函数名称。看起来足够像stats.Distribution实例的对象(即，它们有一个 ppf 方法)也被接受。默认值为 'tukeylambda' 。

退货

shape_value浮动: 概率图相关系数达到最大值时的形状参数。

参见

ppcc_plot, probplot, boxcox

注意事项

Brack关键字用作起点，这在拐角情况下很有用。人们可以使用曲线图来获得最大位置的粗略视觉估计，以便在其附近开始搜索。

参考文献

1: J.J.Filliben，“正态分布的概率图相关系数检验”，“技术计量学”第17卷，第111-117页，1975。
2: 工程统计手册，NIST/SEMATEC，https://www.itl.nist.gov/div898/handbook/eda/section3/ppccplot.htm

示例

首先，我们从形状参数为2.5的威布尔分布生成一些随机数据：

>>> from scipy import stats
>>> import matplotlib.pyplot as plt
>>> rng = np.random.default_rng()
>>> c = 2.5
>>> x = stats.weibull_min.rvs(c, scale=4, size=2000, random_state=rng)

使用威布尔分布为该数据生成PPCC图。

>>> fig, ax = plt.subplots(figsize=(8, 6))
>>> res = stats.ppcc_plot(x, c/2, 2*c, dist='weibull_min', plot=ax)

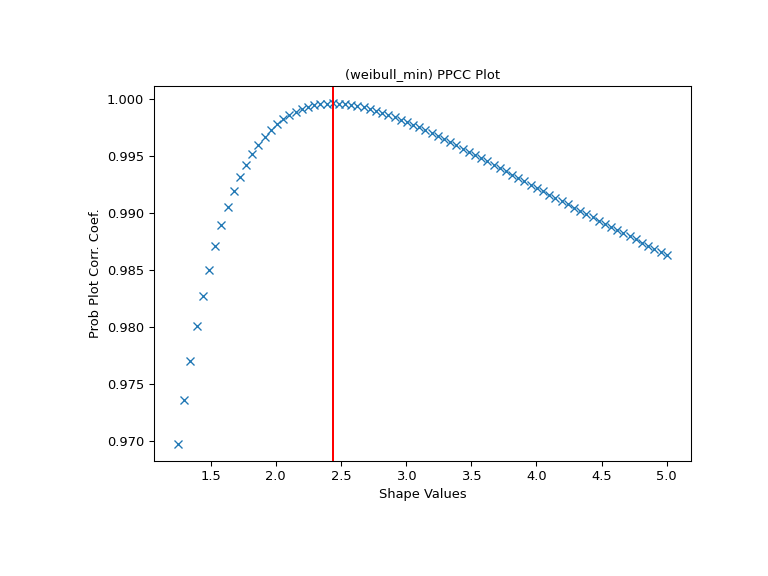
我们计算形状应该达到其最大值的位置，并在那里绘制一条红线。这条线应该与PPCC图形中的最高点重合。

>>> cmax = stats.ppcc_max(x, brack=(c/2, 2*c), dist='weibull_min')
>>> ax.axvline(cmax, color='r')
>>> plt.show()

../../_images/scipy-stats-ppcc_max-1.png

scipy.stats.boschloo_exact

scipy.stats.ppcc_plot