scipy.special.spherical_jn¶

scipy.special.spherical_jn(n, z, derivative=False)[源代码]¶

第一类球面贝塞尔函数或其导数。

定义为 [1],

\[J_n(Z)=\sqrt{\frac{\pi}{2z}}J_{n+1/2}(Z)，\]

哪里 \(J_n\) 是第一类贝塞尔函数。

参数

nint，array_like: 贝塞尔函数的阶数(n>=0)。
z复数或浮点，类似数组: Bessel函数的参数。
derivative布尔值，可选: 如果为True，则返回导数(而不是函数本身)的值。

退货

jnndarray

注意事项

对于大于阶数的实参数，使用升序递归来计算函数 [2]. 对于小的实数或复数，使用与第一类柱面贝塞尔函数的定义关系。

使用以下关系计算导数 [3],

\[ \begin{align}\begin{aligned}J_n‘(Z)=j_{n-1}(Z)-\frac{n+1}{z}j_n(Z)。\\J_0‘(Z)=-j_1(Z)\end{aligned}\end{align} \]

0.18.0 新版功能.

参考文献

1: https://dlmf.nist.gov/10.47.E3
2: https://dlmf.nist.gov/10.51.E1
3: https://dlmf.nist.gov/10.51.E2
AS: 米尔顿·阿布拉莫维茨和艾琳·A·斯特根主编。包含公式、图表和数学表的数学函数手册。纽约：多佛，1972年。

示例

第一类球面Bessel函数 \(j_n\) 接受真实和复杂的第二个论点。它们可以返回复杂类型：

>>> from scipy.special import spherical_jn
>>> spherical_jn(0, 3+5j)
(-9.878987731663194-8.021894345786002j)
>>> type(spherical_jn(0, 3+5j))
<class 'numpy.complex128'>

我们可以从以下注释中验证导数的关系 \(n=3\) 在间隔时间内 \([1, 2]\) ：

>>> from scipy.special import spherical_jn
>>> x = np.arange(1.0, 2.0, 0.01)
>>> np.allclose(spherical_jn(3, x, True),
...             spherical_jn(2, x) - 4/x * spherical_jn(3, x))
True

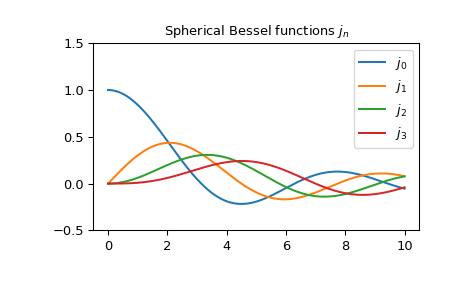
前几位 \(j_n\) 带着实实在在的论据：

>>> import matplotlib.pyplot as plt
>>> from scipy.special import spherical_jn
>>> x = np.arange(0.0, 10.0, 0.01)
>>> fig, ax = plt.subplots()
>>> ax.set_ylim(-0.5, 1.5)
>>> ax.set_title(r'Spherical Bessel functions $j_n$')
>>> for n in np.arange(0, 4):
...     ax.plot(x, spherical_jn(n, x), label=rf'$j_{n}$')
>>> plt.legend(loc='best')
>>> plt.show()

../../_images/scipy-special-spherical_jn-1.png

scipy.special.h2vp

scipy.special.spherical_yn