10.6.1. 地理位置 #
对于生产单位和服务企业来说,由于需求和供给两方面总是存在着空间上分布的差异性,因此, 机构设施地理位置(Geographic Location)的选择和确定对于它们的经济效益和自身的发展具有至关重要的影响作用。
机构设施位置评价和优化, 是通过对于一个设施或者一个设施网络的供给和需求两者之间的相互作用关系进行分析来实现其空间位置分布模式的优化。 机构设施区位评价是对于现有服务设施的空间位置分布模式的评价,机构设施区位优化是对于其最佳位置的搜寻。 克理斯塔勤的中心地理论则为供给区位优化模式的理论研究和经验方法的应用提供了基础框架, 这个理论中的市场区域规模是由供货和服务的范围决定的, 需求和供给两者之间的关系是以距离最小化和利润最大化为基础建立的。 但是,实际应用中的中心地理论,无论是理论方法还是它的经验方法都需要根据具体问题进行具体分析。 例如,与理论中假设的聚落世界相反,区域的人口集中和分散将会对该区域的范围大小产生影响; 同样,消费者的消费行为的选择也会对一个服务中心的功能范围产生影响。 因此,中心地理论虽然提供了一个描述和解释货物服务供给系统和需求行为两方面空间相互作用的主要框架体系, 但它作为一个参考框架,还需要针对特殊情况进行扩充和调整。 图10-16表示了中心地理论应用的概念框架。 图 10.16 中心地理论应用的概念框架 # 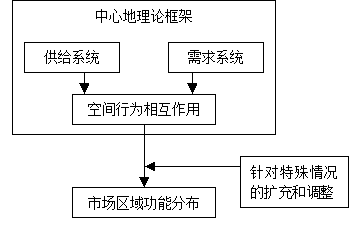
中心地理论的古典模型是对包含单一目标的、且内部需求全部针对这个目标中心的具有均质性的市场功能区域进行空间分析和模拟, 而中心地理论的现代模型则要针对现实世界中那些具有不确定性的、涉及多目标消费行为和复杂供给行为的市场功能区域进行空间分析和模拟。
在对于更具现实性的市场功能行为研究基础之上, 人们研究出了许多能够针对现实世界的市场功能区域进行空间分析和模拟的模型, 如Reily的零售重力模型(Retail Gravitation)、Batty的裂点方程(Breakpoint Equation)、Tobler的价格场和作用风(Price Field and Interaction Wind)以及众多的修正式。 但将重力模型及裂点方程用于分析多点中心地系统则非常艰难,由于缺乏可视性和连续性,因此, 分析结果的成图也很困难。 而Tobler方法是对中心城市场特性的一种半定量描述。 下面,将重点介绍有关定位——配置问题解决方法中的一种空间线性优化模型。
10.6.2. 空间优化模式的定义 #
空间优化模式用于解决位置——分配问题。 位置——分配问题,是在规划重要公共设施的位置及其附属区域时产生的(公共设施, 如医院、幼儿园、游戏场所、养老院、学校、警察局、消防队、急救站、管理设施等, 即属于国家预算范围内的基础设施)。
一个位置一分配问题一般可表述如下:
设有一定数量的居民集中点,这些点被称为需求点(或消费点、居民点),求一定数量的供给点(某种公共设施)以及(或)供给点的需求分配,以完成某个规划目的。
如果已设需求点,求供给点,则涉及位置或定位问题(Location)。
如果已设供给点,求分配,则涉及分配或配置问题(Allocation)。
如果同时求供给点和分配,则涉及位置一分配或定位一配置问题(Location-Allocation)。
通过需求点和供给点之间的分配,供给点的附属区域也就确定了,如图10-17所示。 图 10.17 公共设施的位置及其附属区域(图中实心圆表示需求点,方框表示供给点,供应点附属区域边界为简单的直线,但实际中并非如此) # 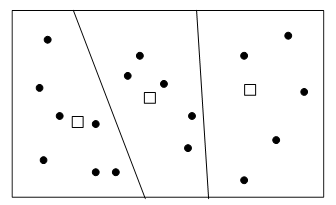
优化模式基本结构由一系列边界条件和一个(或几个,但少见)目标函数组成。 在这些边界条件下,求目标函数的极大值或极小值。 边界条件代表了规划目标所必须满足的划条件,它们代表了对于目标规划区域功能的基本评价; 而优化目标函数(即求目标函数的极值)则代表了一个最大限度可能达到的规划目标。 因此,在边界条件中体现出来的关目标函数的规划条件具有首要意义, 与优化目标函数相应的规划目标的重要性则稍差一些引入目标函数的极大、极小化意义, 在于得到一个定位一配置问题的明确答案(指在一定边界条件下,目标函数有数个可行答案的情况下)。
10.6.3. 空间优化模式的分类 #
按照目标规划的时间范围、问题空间类型、公共设施服务方式、路途费用承担者以及公共设施使用类型等, 可以将空间优化模式进行分类,如图11-18所示。 图 10.18 空间优化模式分类 # 如果规划是在某个时间段(点)上解决位置一分配问题,则采用静态优化模式。 如果规划时间范围包括数个时间段(点),则采用动态优化模式。 动态优化模式虽然形式上易于描述,但在用于解决现实的规划问题时,由于优化目标的规模过大而难以实现, 许多问题可以用静态模式加以圆满解决。 如果所研究地区所有点都可能作为供给点,这就是一个连续性的问题。 但在规划问题上,可作供给点的数目一般是有限的,因此,问题的解决可用离散模式。 规划时间范围及问题空间类型这二个维度非常重要, 因为与它们相应的模式类型在形式结构的复杂性、问题解决的可能性和模式的可操作性上差别很大。 下面将重点讨论“静态一离散空间优化模式”,该模式按照具体规划问题中所遇到的设施类型还可以再进行细分。 如果公共设施只限于在某个确定地点为需求者提供服务,例如学校、幼儿园、养老院、医院、派出所等, 需求者必须亲自前去这些公共设施接受服务,则称这些公共设施的服务方式为“集中式”。 如果公共设施所能提供的服务必须从供给点通过某种运输手段带给需求者,例如消防队、医疗急救中心、警察局等, 则称这些公共设施的服务方式为“分布式”。 当公共设施的服务方式为“集中式”时,需求者一般直接负担自己前去这些公共设施接受服务的路途费用; 当公共设施的服务方式为“分布式”时,需求者为接受服务所支付的费用一般与路途距离无关。 在“集中式”的位置——分配系统中,服务供给点的可接近程度必须从社会公正和机会均等的观点出发, 而在“分布式”的位置——分配系统中工作效率问题的考虑更为重要。 一些公共设施如小学、医院、政府管理机构等, 它们基于相应的法律如小学九年制义务教育、户籍管理制度等以及不可避免的客观事实如看病就医等, 对于需求者具有强制性使用的性质。 这种类型的公共设施由于不存在着竞争意义上的对手,因此,它们将来的需求以及设施规模都是可以预测的, 称这类公共设施为规定性使用类型。 另外一些公共设施如商厦、饭店、宾馆、公园、体育馆等社会基础设施,属于需求自愿使用的设施类型。 这类设施的供给与需求矛盾可能会变的非常突出,因此,它们将来的需求以及设施的规模难以预测, 它们的需求者经常根据运输费用的变化而发生变化。 这类设施定位时,优先考虑选择居民数量增加潜力较大的地点。 和公共设施的使用类型一样,需求点的分配类型也可以是自愿或规定的。 在“分布式”的位置一分配系统中,需求点的分配类型属于规定型, 属于公共设施的由需求点组成的附属区域一般是确定的(既使需求者是出于自愿的);在“集中式”的位置一分配系统中, 需求点的分配类型属于自愿型,属于公共设施的由需求点组成的附属区域一般是不确定的。 比较困难的是,在需求点自愿分配的情况下估计各个供给点的附属区域及公共设施设置的规模。 如何将使用者分配至供给点,可以用生产和吸引力有限的空间作用模式大概估算出来。 需求点的规定分配与不相连的附属区域相对应,需求点的自愿分配与相连的附属区域相对应。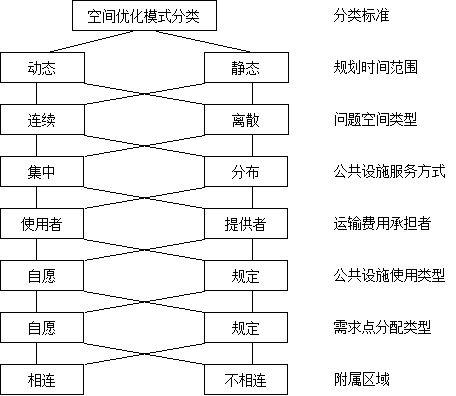
规划时间范围 #
问题空间类型 #
公共设施服务方式 #
运输费用承担者 #
公共设施的使用类型 #
需求点的分配类型 #
附属区域类型 #
10.6.4. 静态——离散空间优化模式的数学表达:线性规划 #
有关静态——离散的定位——配置问题是在规划重要公共设施的位置及其附属区域时出现的。 静态——离散的位置——配置问题须考虑很多潜在的供给点, 并且位置和附属区域的确定将在长时间内处于不变的状态。
在空间优化过程中,如果目标函数和边界条件都是线性的, 则采用的数学工具是线性规划 [1]_(LinearProgramming)。 所谓线性规划,是指在一组线性的等式和不等式的约束下,求一个线性函数的最大值或最小值的问题。
线性规划的一般形式为::
目标:
min
c_1
x_1
+
c_2
x_2
+…
…+c_n
x_n
约束条件:
a_11
x_1
+
c_12
x_2
+…
…+c_1n
x_n
≤c_1
… …
a_m1
x_1
+
c_m2
x_2
+…
…+c_mn
x_n
≤c_1
x_1,
x_2…
…
x_n
≥0
下面一个例子属于产销区划,就可以用线性规划解决,有A、B、C三个产地,产量分别为50、30、20, 对应销地I、II、III,需要量分别为40、40、20。 首先通过最短路径分析,得到如表10-6描述的运费。
表10-6:资源分配的运费表(∞表示不连通)
I | II | III | |
A | 2 | 3 | 5 |
B | ∞ | 1.5 | 8 |
C | 2 | 4 | ∞ |
问题是:如何确定其供应关系,使得总运费最少。 假定
x_11
表示从A到I的运量,
x_12
表示从A到II的运量, 依次类推。 则问题可以描述为:
Object:
min``2x_11 +3x_12 +5x_13 +1.5x_22 +8x_23 +2x_31 +4x_32``
Constraint:
x_11 + x_12 +x_13 =50
x_22 +x_23 =30
x_31 +x_32 =20
x_11 +x_31 =40
x_12 +x_22 +x_32 =40
x_13 +x_23 =20
x_11,`x_12,`x_13,`x_22,`x_23,`x_31,`x_≥0`
目前已经有许多成熟的解决线性规划的方案,如图解法、单纯形法等等。 上述供销区划的答案如表10-7所示,总运费为255。
表10-7:资源分配的运量
I | II | III | |
A | 20 | 10 | 20 |
B | 0 | 30 | 0 |
C | 20 | 0 | 0 |
基因算法(Genetic Algorithm):
基因算法是最近提出的用于解决优化问题的方法,它通过对一个集合的变量值进行优化, 得到可以定量描述优劣的目标。 量化描述目标合适程度的思路来自于达尔文的进化论,在进化过程中, 不同代生物染色体的基因的内容和形式都在发生变化,使得生物更能够适合于生存环境。 在基因算法中,是通过不同方式的组合以及修改数值以改变变量,这类似于生物的配对和变异。 通过比较合适指标,测试改变变量后的计算结果,保留“有利的”组合,并进行进一步的修改。 一种理想的结果是:保留下来的改变优于其它的组合和改变,通过不断的迭代过程,可以使得一个优化的结果。 基因算法的成败依赖于以何种方式来模拟各种形式的染色体,并使其不断进化,以增加它在最优解中的存活几率。 存活下来的染色体一般都对应于一个局部极值,而后者可以导致全局的最优解。
在一个基因算法中,要确定的内容包括:
基因操作,如配对和变异;
策略性的参数:如配对和变异发生的几率;
表现模式:如对基因的编码等等。
在GIS中,基因算法可以应用于空间相互作用(SpatialInteraction)建模, 后者可以应用于公共设施,如商店、医院等的区位。