GIS空间分析与空间动态建模

目前，GIS已被广泛接受为管理、存储、查询分析有关地理空间分布的信息的成熟的工具和技术，近年来对GIS提出的越来越多的挑战是将这个本质上静态的系统变为支持模拟空间——时间过程的经济可行的工具，为科学研究和资源管理服务。目前大多数GIS软件不能支持多学科领域的动态过程计算模型，包括水文、生态等地学和生物科学，大多数GIS系统只是为模型提供输入参数和显示输出结果。集成GIS空间分析与空间动态建模困难的原因在于：

  1. 领域科学家、数据收集者和GIS技术人员存在着重要的概念差异，导致他们对现实世界抽象方式、如何用计算机组织和结构化数据的方式存在很大差异。

  2. GIS记录、存储的数据可能不是模型最适合的数据格式，有时需要进行转换。

  3. 除非对计算机编程非常熟悉，否则编写一个空间过程的动态模型是一个困难的很花费时间的过程。

  4. 许多GIS软件的可视化方法并不支持对模型结果的交互式空间——时间表现。

  5. 满足许多科学家要求的、快速有效的模拟动态模型的开放系统模拟方法（如元胞自动机），在GIS实现的很少。

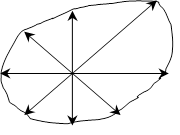
所谓空间动态模型是指现实世界中地球表面特定位置上的某些属性或状态因其驱动力随时间变化而发生改变的一种数学模拟。从计算的角度考虑，空间动态模型就是要计算各空间单元随其时间序列信息或驱动力的变化而产生新状态或属性值。各时刻的状态或属性可以用计算机以动画的形式进行显示，其实质仍然是图形代数和地图模型的自然延伸。但由于GIS空间分析功能的语义限制，不能直接支持空间动态建模的操作元语，所以目前很多模型都是在GIS支持下，经过扩展或修改，采取与GIS相互结合的方式实现的。

GIS与空间动态模型的结合方式

GIS与空间动态模型的结合主要有三种方式：松散结合，交互界面和镶嵌结合。松散结合主要用于模型与GIS各自开发的情形，在这种结合中，先用GIS查询，预处理空间数据，然后按模型所需的格式将其输入模型，模型计算的结果再转为GIS文件格式，进行显示和分析。松散结合的优点在于无须改变模型的代码，不足之处在于大量的数据管理和转换工作，要求模型和GIS两方面的专门知识。第二种结合方式是开发交互界面。这种结合就是开发支持模型的GIS数据库，同时开发一个界面，既可以为模型提供输入数据，又能利用模型结果进行处理和演示，所有的数据转换是通过交互界面自动进行的。此类结合的实例最多，交互界面的优点在于提供了模型与GIS平台的接口，节省了大量数据输入输出工作。不足在于编程和数据管理上的投资比较大，用户修改和重写模型的难度大。第三种方式是镶嵌结合。这类结合要么是一个简单的GIS嵌入到一个复杂的模型系统以提供结果显示和交互控制功能，要么是用GIS的函数命令重写模型。这样模型和GIS同在一个系统中，二者共用同一个数据库，不存在数据交换问题。当模型对GIS的功能要求不多时常采用前一种镶嵌方法。而用GIS函数命令重写模型的优点在于用户可以建立自己的模型，不足在于GIS的命令和函数有时不能满足建立模型的所有需要。

元胞自动机简介

元胞自动机（Cellular Automata，CA）是定义在一个具有离散、有限状态的元胞组成的元胞空间上的，按照一定局部规则，在离散的时间维上演化的动力学系统。元胞自动机的基本单元是元胞（Cell），每个元胞具有一个状态，这个状态只能取有限状态集中的一个，例如“生”或“死”，或者256种颜色中的一种等等；这些元胞规则地排列在被称为“元胞空间”的空间格网上；它们各自的状态随着时间变化，根据一个局部的规则来进行更新，即一个元胞在某时刻的状态取决于且只取决于该元胞周围邻域元胞的状态；元胞空间内的元胞依照此局部规则进行同步的状态更新，整个元胞空间则表现为在离散的时间维上变化。

元胞自动机的最基本的组成包括元胞（Cell），元胞空间（Lattice），邻域（Neighbor），规则（Rule）。元胞自动机可以视为由一个元胞空间和定义在该空间的变换函数所组成。标准的元胞自动机是一个四元组：

A=（d, S, N, f）

A代表一个元胞自动机系统；d是一个正整数，表示元胞自动机的维数；S是元胞的有限的离散的状态集合；N表示一个所有邻域内元胞的组合，即包含个不同元胞状态的空间矢量，记为：

N = ( s:sub:`1`, s:sub:`2`, s:sub:`3`, ..., s:sub:`n`)

n是邻域内元胞的个数；si∈Z（整数集合），i∈(1,2,...n)；f是变化规则，为将Sn映射到S上的一个局部转换函数。所有的元胞位于d维空间上，其位置可用一个d元的整数矢量Zd来确定。

一般地，元胞自动机的基本模型具有五个主要特征：

  1. 它们由元胞的离散格局构成；

  2. 它们在离散时间步序内演化；

  3. 每一元胞的状态均在同一有限集中取值；

  4. 每一元胞的状态依同一确定的法则演化；

  5. 元胞状态的取值法则仅依赖于其自身及其周围邻域元胞的状态值。

元胞自动机虽然是产生于并行计算机结构的一种理论模型，但它还可用来描述具有很大自由度的离散系统，可视为偏微分方程离散化的理想形式。元胞自动机模型可用来模拟研究很多的现象，包括信息传递、计算、构造、生长、复制、竞争与进化等，同时，它为动力学系统理论中有关秩序、紊动、混沌、非对称、分形等系统整体行为与现象的研究提供了一个有效的模型工具。

元胞自动机模型具有很强的灵活性和开放性，它不是一个简单的数理方程，而更象是一种方法论。各领域专家可对模型的各个组成部分进行灵活的扩展，建立适合模拟各种专题现象的扩展模型，这是元胞自动机广泛应用于社会、经济、环境、地学、生物等领域的原因。尤其需要说明的是当元胞自动机在二维空间上时，元胞空间结构与栅格GIS数据结构高度相容，因此使用栅格GIS结合元胞自动机模型，可以用于离散时间和离散空间的框架下对复杂时空动态过程进行模拟。下面以一个林火模型的实例对GIS与元胞自动机模型的结合，模拟林火时空动态蔓延过程。

元胞自动机模拟林火蔓延模型

森林火灾是一种常见的自然灾害，当森林火灾发生时，快速准确地模拟和预测火势的蔓延和发展，对于及时部署灭火力量，搬迁居民，减少人民生命财产损失，具有重大的实际意义。林火模型中最成功的是Rothermel的林火蔓延模型，模型主要考虑的因素有：

  1. 森林的材质：包括燃料物质载荷、燃料深度、燃料粒子密度、热容量、灭火所需湿度等。

  2. 燃料湿度、空气温度。

  3. 风速、风向。

  4. 地形坡度。

模型可以计算林火的蔓延速率，火灾的强度、范围和面积等。

基于该模型的框架，一些研究人员结合元胞自动机原理和GIS，建立了新的林火模型。该模型是一个二维元胞自动机模型，基本假设条件有：森林均匀分布，材质均一；地形为平原，不考虑地形影响；风向随机，即不考虑风向影响。模型的特征如下：

元胞空间：元胞空间是将实际研究区按照一定分辨率划分的离散网格，格网单元为正方形单元，与GIS栅格数据结构一致。

元胞状态：每个元胞具有四种状态，0代表无森林覆盖，1代表未燃森林，2，代表正在燃烧森林，3代表已烧过的森林。

邻域定义：每个元胞以8个相邻元胞作为其邻域元胞。

转换规则：林火蔓延规则，即在燃元胞的扩展规则。我们假定在燃元胞可以一次点燃周围邻居中的所有未燃森林，具体规则如下：

如果ni,j ( t ) = 0或 ni,j ( t ) = 3，则ni,j ( t +1 ) = ni,j ( t ) ；

如果ni,j ( t ) = 2，则ni,j ( t +1 ) = 3 ；

如果ni,j ( t ) = 1且 n‘ ( t ) = 2（n‘为邻居元胞集合中的元素），则ni,j ( t +1 ) = 2；

否则，ni,j ( t +1 ) = 1。

这是一个对现实高度简化的林火蔓延模型，蔓延表现为由火点向四周成圆形扩散，基本上反映了一个理想化林火蔓延过程。实际上这个模型是一个最基本的二维通用扩散模型，可以在此基础上，加以改进、扩展，用来模拟疾病传播、污水扩散等现象。

为了更加真实的模拟林火行为过程，对上面的理想模型进行了扩展，扩展后具体模型如下。

元胞空间：与理想模型一致，只是在应用中与数字高程模型、遥感影象等数据的分辨率相匹配。

元胞状态：元胞的状态除表示森林燃烧状态外，还扩展了森林材质、湿度、地形坡度、风速风向等变量。另外为了更精确描述燃烧的过程，燃烧状态又细分成三个子状态，其中21表示刚刚被点燃的森林，22表示火势旺盛的森林，23表示由明火转向暗火的森林（逐渐熄灭）。由于不同材质的森林在各个燃烧阶段的持续时间不同，气温和湿度也会对燃烧阶段的持续时间产生影影响，所以在森林着火之前，需要确定各个森林元胞一旦着火后，处于燃烧三个子阶段的时间（可以通过GIS再分类命令实现）RT1，RT2，RT3。其它三个状态不变，还是0代表无森林覆盖，1代表未燃森林，3代表已烧过的森林。

邻域定义：每个元胞以8个相邻元胞作为其邻域元胞。

转换规则：林火蔓延规则进行了扩展。假定只有状态为22的元胞，燃烧正旺的森林才能点燃其邻域元胞；状态为21的元胞刚被点燃，火势较小不会点燃周围元胞；状态为23的元胞则由于火势减弱，也无法点燃周围元胞。具体的转换规则如下：

如果ni,j ( t ) = 0或 ni,j ( t ) = 3，则ni,j ( t +1 ) = ni,j ( t ) ；

如果ni,j ( t ) = 21，则有

若RTi,j>RT1i,j ，则ni,j ( t +1 ) = 22 ；

否则ni,j ( t +1 ) = 21，RTi,j= RTi,j+1；

如果ni,j ( t ) = 22，则有

若RTi,j> RT1i,j +RT2i,j ，则ni,j ( t +1 ) = 23；

否则ni,j ( t +1 ) = 22，RTi,j= RTi,j+1；

如果ni,j ( t ) = 23，则有

若RTi,j>= RT1i,j +RT2i,j +RT3i,j，则ni,j ( t +1 ) = 3；

否则ni,j ( t +1 ) = 23，RTi,j= RTi,j+1；

如果ni,j ( t ) = 1且 n‘ ( t ) = 22（n‘为邻居元胞集合中的元素），

若当前元胞被点燃的可能性超过设定的概率水平后，则ni,j ( t +1 ) = 21，RTi,j= 0；

否则，ni,j ( t +1 ) = 1。

其中，计算森林元胞被邻域元胞点燃的可能性的计算方法是：

首先得到元胞状态为22的各个元胞点燃周围森林的可能性向量Pk，如图10-15所示：

../../_images/img_112.png

图10-15：状态为22的元胞点燃周围森林的可能性向量图

然后计算当前森林元胞被点燃的可能性是它的所有相邻元胞点燃它的概率和。若超过了设定的概率水平，则可用随机数的产生方法来确定当前元胞是否被点燃。

至此，一个较为精确的林火蔓延的动态模型构建完成。这样将模型集成到GIS系统中，在空间数据库、遥感影象、数字高程模型等数据的支持下，提取合理的模型参数，对森林不同地点、不同天气条件下，一旦着火后的林火蔓延过程进行动态模拟和预测，对森林防火、火灾救险工作有很大的应用价值。

元胞自动机与GIS集成应用中的局限性

1）简单性与真实性的矛盾问题

元胞自动机是对现实世界的高度抽象和概括，它能简洁直观地模拟空间复杂系统的动态演化，但同时人们不仅会怀疑现实系统是不是这样演化的，真实性是元胞自动机模型面临的最大质疑。问题在于：元胞自动机只考虑元胞之间的局部作用，而没考虑元胞空间的宏观作用，因而忽略了现实系统的宏观作用因素；元胞自动机的因素层过于单一，元胞状态的变化取决于自身和邻域元胞的状态组合，从而忽略了其它因素的影响；标准元胞自动机的转换规则是确定性的，而现实系统的行为并非是确定性的，往往表现为某种倾向和可能性。所以在实际应用中，需要在简单性和真实性之间寻找一个平衡点，避免模型过于简单，造成结果的不真实，又要防止模型过于复杂，而失去了模型本身的意义和优势。

2）空间划分问题

元胞自动机是建立在离散、规则的空间划分基础上的，但如何确定合适的空间分辨率却是元胞自动机应用的一个难题。尤其是在多种地理实体共存的系统中，不同的实体有着不同的空间尺度，如何确定一个同一的空间分辨率，对于元胞自动机建模更为困难。另外，在不同的空间分辨率下，地理系统单元所表现出的规律也有所不同，因此，如何确定适当的分辨率，并进一步制定合理的模型规则是元胞自动机建模的一个难题。

3）时间对应问题

在元胞自动机模型中，时间是一个抽象的概念，从模型中的T时刻到T+1时刻对应的时间单位不明确，而不同元胞在不同状态下持续的时间也很难确定。

4）转换规则定义问题

合理的规则是模型效果的关键，在元胞自动机模型中，规则是针对抽象空间划分单元的，反映了单元间局部的相互作用。此局部规则与传统的宏观规律，既有联系，又存在差别，而且找到一个确定性的规则的难度相当大。

5）与GIS集成的问题

GIS系统的支持是地理系统建模研究的必要条件，虽然元胞自动机模型与栅格GIS在空间数据结构上存在较大的相似性，但元胞自动机是一个时空动态模型，而目前GIS本质上是一个静态系统，支持动态模拟的功能较弱，二者的集成有一定的困难。如何将二者紧密的集成，是阻碍元胞自动机在地理系统研究中应用的一个难题。