大部分GIS软件是以分层的方式组织地理景观,将地理景观按主题分层提取, 同一地区的整个数据层集表达了该地区地理景观的内容。 每个主题层,可以叫做一个数据层面。 数据层面既可以用矢量结构的点、线、面图层文件方式表达,也可以用栅格结构的图层文件格式进行表达。
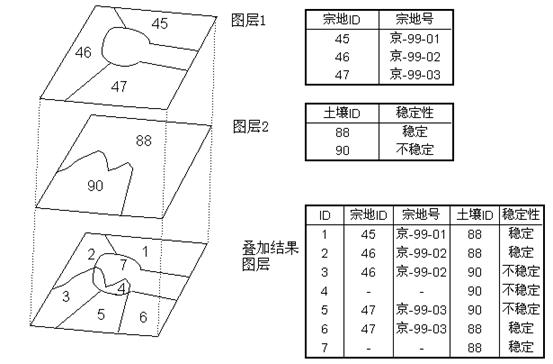
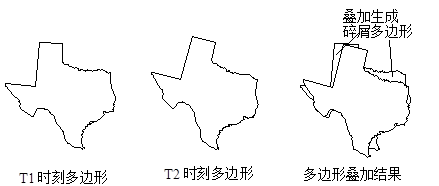
叠加分析是地理信息系统最常用的提取空间隐含信息的手段之一。 该方法源于传统的透明材料叠加,即将来自不同的数据源的图纸绘于透明纸上,在透光桌上将其叠放在一起, 然后用笔勾出感兴趣的部分—提取出感兴趣的信息。 地理信息系统的叠加分析是将有关主题层组成的数据层面,进行叠加产生一个新数据层面的操作, 其结果综合了原来两层或多层要素所具有的属性。 叠加分析不仅包含空间关系的比较,还包含属性关系的比较。 地理信息系统叠加分析可以分为以下几类: 视觉信息叠加、点与多边形叠加、线与多边形叠加、多边形叠加、栅格图层叠加。 视觉信息叠加是将不同侧面的信息内容叠加显示在结果图件或屏幕上,以便研究者判断其相互空间关系, 获得更为丰富的空间信息。 地理信息系统中视觉信息叠加包括以下几类: 点状图,线状图和面状图之间的叠加显示。 面状图区域边界之间或一个面状图与其他专题区域边界之间的叠加。 遥感影象与 专题地图 的叠加。 专题地图 与数字高程模型( DEM )叠加显示立体专题图。 视觉信息叠加不产生新的数据层面,只是将多层信息复合显示,便于分析。 点与多边形叠加,实际上是计算多边形对点的包含关系。 矢量结构的GIS能够通过计算每个点相对于多边形线段的位置,进行点是否在一个多边形中的空间关系判断。 在完成点与多边形的几何关系计算后,还要进行属性信息处理。 最简单的方式是将多边形属性信息叠加到其中的点上。 当然也可以将点的属性叠加到多边形上,用于标识该多边形,如果有多个点分布在一个多边形内的情形时, 则要采用一些特殊规则,如将点的数目或各点属性的总和等信息叠加到多边形上。 通过点与多边形叠加,可以计算出每个多边形类型里有多少个点,不但要区分点是否在多边形内, 还要描述在多边形内部的点的属性信息。 通常不直接产生新数据层面,只是把属性信息叠加到原图层中, 然后通过属性查询间接获得点与多边形叠加的需要信息。 例如一个中国政区图(多边形)和一个全国矿产分布图(点),二者经叠加分析后, 并且将政区图多边形有关的属性信息加到矿产的属性数据表中,然后通过属性查询,可以查询指定省有多少种矿产, 产量有多少; 而且可以查询,指定类型的矿产在哪些省里有分布等信息。 线与多边形的叠加,是比较线上坐标与多边形坐标的关系,判断线是否落在多边形内。 计算过程通常是计算线与多边形的交点,只要相交,就产生一个结点,将原线打断成一条条弧段, 并将原线和多边形的属性信息一起赋给新弧段。 叠加的结果产生了一个新的数据层面,每条线被它穿过的多边形打断成新弧段图层, 同时产生一个相应的属性数据表记录原线和多边形的属性信息。 根据叠加的结果可以确定每条弧段落在哪个多边形内,可以查询指定多边形内指定线穿过的长度。 如果线状图层为河流,叠加的结果是多边形将穿过它的所有河流打断成弧段,可以查询任意多边形内的河流长度, 进而计算它的河流密度等;如果线状图层为道路网,叠加的结果可以得到每个多边形内的道路网密度, 内部的交通流量,进入、离开各个多边形的交通量,相邻多边形之间的相互交通量。 多边形叠加是GIS最常用的功能之一。 多边形叠加将两个或多个多边形图层进行叠加产生一个新多边形图层的操作,其结果将原来多边形要素分割成新要素, 新要素综合了原来两层或多层的属性。 如图8-11所示: 图 8.11 图8-11:多边形叠加分析 # 进行多个多边形的叠加运算,在参与运算多边形所构成的属性空间(就图10而言,为宗地ID,宗地号,土壤ID, 稳定性)内,每个结果多边形内部的属性值是一致的, 可以称为最小公共地理单元(Least Common Geographic Unit,LCGU)。 叠加过程可分为几何求交过程和属性分配过程两步。 几何求交过程首先求出所有多边形边界线的交点,再根据这些交点重新进行多边形拓扑运算, 对新生成的拓扑多边形图层的每个对象赋一多边形唯一标识码,同时生成一个与新多边形对象一一对应的属性表。 由于矢量结构的有限精度原因,几何对象不可能完全匹配, 叠加结果可能会出现一些碎屑多边形(Silver Polygon),如图8-12所示。 通常可以设定一模糊容限以消除它。 图 8.12 图8-12:多边形叠加产生碎屑多边形 # 多边形叠加结果通常把一个多边形分割成多个多边形, 属性分配过程最典型的方法是将输入图层对象的属性拷贝到新对象的属性表中,或把输入图层对象的标识作为外键, 直接关联到输入图层的属性表。 这种属性分配方法的理论假设是多边形对象内属性是均质的,将它们分割后,属性不变。 也可以结合多种统计方法为新多边形赋属性值。 多边形叠加完成后,根据新图层的属性表可以查询原图层的属性信息, 新生成的图层和其它图层一样可以进行各种空间分析和查询操作。 根据叠加结果最后欲保留空间特征的不同要求,一般的GIS软件都提供了三种类型的多边形叠加操作, 如图8-13所示: 图 8.13 图8-13:多边形的不同叠加方式 # 栅格数据结构空间信息隐含属性信息明显的特点,可以看作是最典型的数据层面, 通过数学关系建立不同数据层面之间的联系是GIS提供的典型功能。 空间模拟 尤其需要通过各种各样的方程将不同数据层面进行叠加运算,以揭示某种空间现象或空间过程。 例如土壤侵蚀强度与土壤可蚀性,坡度,降雨侵蚀力等因素有关,可以根据多年统计的经验方程, 把土壤可蚀性、坡度、降雨侵蚀力作为数据层面输入,通过数学运算得到土壤侵蚀强度分布图。 这种作用于不同数据层面上的基于数学运算的叠加运算,在地理信息系统中称为地图代数。 地图代数功能有三种不同的类型: 基于常数对数据层面进行的代数运算; 基于数学变换对数据层面进行的数学变换(指数、对数、三角变换等); 多个数据层面的代数运算(加、减、乘、除、乘方等)和逻辑运算(与、或、非、异或等)。 下面给出一个地图代数的典型例子。 有一个森林地区融雪经验模型: 式中,M是融雪速度(厘米/天),T是空气温度,D是露点温度。 根据此方程,使用该地区的气温和露点温度分布图层,就能计算该地区融雪速率分布图。 计算过程是先分别把温度分布图乘以0.19和露点温度分布图乘以0.17,再把得到的结果相加。 需要说明的是地图代数在形式和概念上都比较简单,使用起来方便灵活,但把图层作为代数公式的变量进行计算, 在实现的技术上难度较大。 栅格图层叠加的另一形式是二值逻辑叠加,常作为栅格结构的数据库查询工具。 数据库查询就是查找数据库中已有的信息,例如:基于位置信息查询如已知地点的土地类型, 以及基于属性信息的查询如地价最高的位置; 比较复杂的查询涉及多种复合条件,如查询所有的面积大于10公顷且邻近工业区的全部湿地。 这种数据库查询通常分为两步,首先进行再分类(见第三节)操作,为每个条件创建一个新图层,通常是二值图层, 1代表符合条件,0表示所有不符合条件。 第二步进行二值逻辑叠加操作得到想查询的结果。 逻辑操作类型包括与、或、非、异或。 8.5.1. 视觉信息叠加 #
8.5.2. 点与多边形叠加 #
8.5.3. 线与多边形叠加 #
8.5.4. 多边形叠加 #
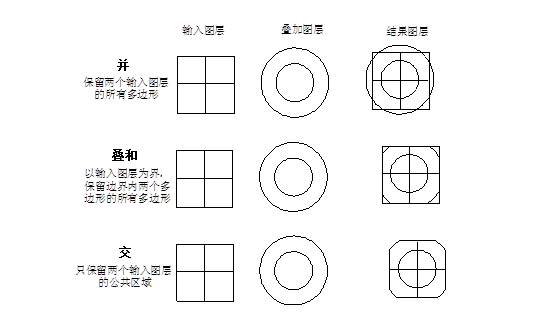
8.5.5. 栅格图层叠加 #