8.4. 缓冲区分析

邻近度（Proximity）描述了地理空间中两个地物距离相近的程度，其确定是空间分析的一个重要手段。交通沿线或河流沿线的地物有其独特的重要性，公共设施（商场，邮局，银行，医院，车站，学校等）的服务半径，大型水库建设引起的搬迁，铁路，公路以及航运河道对其所穿过区域经济发展的重要性等，均是一个邻近度问题。缓冲区分析是解决邻近度问题的空间分析工具之一。

所谓缓冲区就是地理空间目标的一种影响范围或服务范围。从数学的角度看，缓冲区分析的基本思想是给定一个空间对象或集合，确定它们的邻域，邻域的大小由邻域半径R决定。因此对象 O_i 的缓冲区定义为：

即对象 O_i 的半径为 R 的缓冲区为距 O_i 的距离 d 小于 R 的全部点的集合。 d 一般是最小欧氏距离，但也可是其它定义的距离。对于对象集合

其半径为R的缓冲区是各个对象缓冲区的并，即：

图8-6为点对象、线对象、面对象及对象集合的缓冲区示例。

/media/sphinx_tuto/img/img_1_x7p.png — 图 8.6 点、线、多边形的缓冲区 #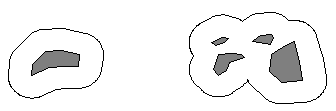

另外还有一些特殊形态的缓冲区，如点对象有三角形，矩形和圈形等，对于线对象有双侧对称，双侧不对称或单侧缓冲区，对于面对象有内侧和外侧缓冲区。这些适合不同应用要求的缓冲区，尽管形态特殊，但基本原理是一致的。

缓冲区计算的基本问题是双线问题。双线问题有很多另外的名称，如图形加粗，加宽线，中心线扩张等，它们指的都是相同的操作。

1）角分线法

双线问题最简单的方法是角分线法（简单平行线法）。算法是在轴线首尾点处，作轴线的垂线并按缓冲区半径R截出左右边线的起止点；在轴线的其它转折点上，用与该线所关联的前后两邻边距轴线的距离为R的两平行线的交点来生成缓冲区对应顶点。如图8-7所示。

/media/sph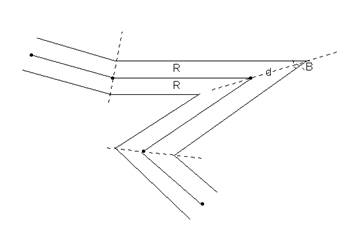inx_tuto/img/img_2_xi8.jpg — 图 8.7 角平分线法 #

角分线法的缺点是难以最大限度保证双线的等宽性，尤其是在凸侧角点在进一步变锐时，将远离轴线顶点。根据上图，远离情况可由下式表示：

当缓冲区半径不变时，d随张角B的减小而增大，结果在尖角处双线之间的宽度遭到破坏。

因此，为克服角分线法的缺点，要有相应的补充判别方案，用于校正所出现的异常情况。但由于异常情况不胜枚举，导致校正措施繁杂。

2）凸角圆弧法

在轴线首尾点处，作轴线的垂线并按双线和缓冲区半径截出左右边线起止点；在轴线其它转折点处，首先判断该点的凸凹性，在凸侧用圆弧弥合，在凹侧则用前后两邻边平行线的交点生成对应顶点。这样外角以圆弧连接，内角直接连接，线段端点以半圆封闭。如图8-8所示。

/media/sph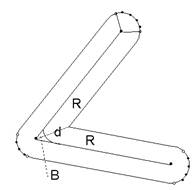inx_tuto/img/img_3_x2k.jpg — 图 8.8 凸角圆弧法 #

在凹侧平行边线相交在角分线上。交点距对应顶点的距离与角分线法类似公式：

该方法最大限度的保证了平行曲线的等宽性，避免了角分线法的众多异常情况。

该算法非常重要的一环是折点凸凹性的自动判断。此问题可转化为两个矢量的叉积：把相邻两个线段看成两个矢量，其方向取坐标点序方向。若前一个矢量以最小角度扫向第二个矢量时呈逆时针方向，则为凸顶点，反之为凹顶点。具体算法过程如下：

由矢量代数可知，矢量AB，BC可用其端点坐标差表示（9-9）：

/media/sphinx_tuto/img/img_4_xuf.png — 图 8.9 采用向量叉乘判断向量排列 #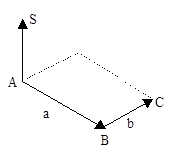

矢量代数叉积遵循右手法则，即当ABC呈逆时针方向时，S为正，否则为负。

若S>0，则ABC呈逆时针，顶点为凸；
若S<0 < p ，则abc呈顺时针，顶点为凹；>
若S=0，则ABC三点共线。

对于简单情形，缓冲区是一个简单多边形，但当计算形状比较复杂的对象或多个对象集合的缓冲区时，就复杂得多。为使缓冲区算法适应更为普遍的情况，就不得不处理边线自相交的情况。当轴线的弯曲空间不容许双线的边线无压盖地通过时，就会产生若干个自相交多边形。图8-10给出一个缓冲区边线自相交的例子。

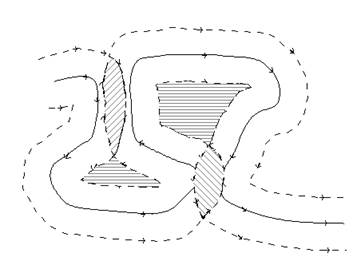
/media/sphinx_tuto/img/img_5_xrc.jpg — 图 8.10 缓冲区边界相交的情况 #

自相交多边形分为两种情况：岛屿多边形和重叠多边形。岛屿多边形是缓冲区边线的有效组成部分；重叠多边形不是缓冲区边线的有效组成，不参与缓冲区边线的最终重构。对于岛屿多边形和重叠多边形的自动判别方法，首先定义轴线坐标点序为其方向，缓冲区双线分成左右边线，左右边线自相交多边形的判别情形恰好对称。对于左边线，岛屿自相交多边形呈逆时针方向，重叠自相交多边形呈顺时针方向；对于右边线，岛屿多边形呈顺时针方向，重叠多边形呈逆时针方向。

当存在岛屿和重叠自相交多边形时，最终计算的边线被分为外部边线和若干岛屿。对于缓冲区边线绘制，只要把外围边线和岛屿轮廓绘出即可。对于缓冲区检索，在外边线所形成的多边形检索后，要再扣除所有岛屿多边形的检索结果。

基于栅格结构也可以作缓冲区分析，通常称为推移或扩散（Spread）。推移或扩散实际上是模拟主体对邻近对象的作用过程，物体在主体的作用下在一阻力表面移动，离主体越远作用力越弱。例如可以将地形、障碍物和空气作为阻力表面，噪声源为主体，用推移或扩散的方法计算噪声离开主体后在阻力表面上的移动，得到一定范围内每个栅格单元的噪声强度。

本文链接： 8.4. 缓冲区分析

《地理信息系统原理、技术与方法》 97

最近几年来，地理信息系统无论是在理论上还是应用上都处在一个飞速发展的阶段。 GIS被应用于多个领域的建模和决策支持，如城市管理、区划、环境整治等等，地理信息成为信息时代重要的组成部分之一； “数字地球”概念的提出，更进一步推动了作为其技术支撑的GIS的发展。与此同时，一些学者致力于相关的理论研究，如空间感知、空间数据误差、空间关系的形式化等等。这恰好说明了地理信息系统作为应用技术和学科的两个方面，并且这两个方面构成了相互促进的发展过程。