7.2.1. 栅格数据结构 #
定义 #
栅格结构是最简单最直接的空间数据结构,是指将地球表面划分为大小均匀紧密相邻的网格阵列, 每个网格作为一个象元或象素由行、列定义,并包含一个代码表示该象素的属性类型或量值, 或仅仅包括指向其属性记录的指针。 因此,栅格结构是以规则的阵列来表示空间地物或现象分布的数据组织, 组织中的每个数据表示地物或现象的非几何属性特征。 如图7-4所示,在栅格结构中,点用一个栅格单元表示; 线状地物沿线走向的一组相邻栅格单元表示,每个栅格单元最多只有两个相邻单元在线上; 面或区域用记有区域属性的相邻栅格单元的集合表示,每个栅格单元可有多于两个的相邻单元同属一个区域。 遥感影像属于典型的栅格结构,每个象元的数字表示影像的灰度等级。
(a)点 (b)线 (c)面 图 7.4 点、线、区域的格网 # 
特点 #
栅格结构的显著特点是: 属性明显,定位隐含,即数据直接记录属性的指针或属性本身,而所在位置则根据行列号转换为相应的坐标, 也就是说定位是根据数据在数据集中的位置得到的。 如图7-4-(a)所示,数据2表示属性或编码为2的一个点,其位置由其所在的第3行、第4列交叉得到的。 由于栅格结构是按一定的规则排列的,所表示的实体的位置很容易隐含在格网文件的存储结构中, 在后面讲述栅格结构编码时可以看到,每个存储单元的行列位置可以方便地根据其在文件中的记录位置得到, 且行列坐标可以很容易地转为其他坐标系下的坐标。 在格网文件中每个代码本身明确地代表了实体的属性或属性的编码,如果为属性的编码, 则该编码可作为指向实体属性表的指针。 图7-4-(a)表示了代码为2的点实体,图7-4-(b)表示了一条代码为6的线实体, 而图7-4-(c)则表示了三个面实体或称为区域实体,代码分别为4、7和8。 由于栅格行列阵列容易为计算机存储、操作和显示,因此这种结构容易实现,算法简单,且易于扩充、修改, 也很直观,特别是易于同遥感影像的结合处理,给地理空间数据处理带来了极大的方便。
栅格结构表示的地表是不连续的,是量化和近似离散的数据。 在栅格结构中,地表被分成相互邻接、规则排列的矩形方块(特殊的情况下也可以是三角形或菱形、六边形等), 每个地块与一个栅格单元相对应。 栅格数据的比例尺就是栅格大小与地表相应单元大小之比。 在许多栅格数据处理时,常假设栅格所表示的量化表面是连续的,以便使用某些连续函数。 由于栅格结构对地表的量化,在计算面积、长度、距离、形状等空间指标时,若栅格尺寸较大,则造成较大的误差, 由于在一个栅格的地表范围内,可能存在多于一种的地物,而表示在相应的栅格结构中常常是一个代码。 也类似于遥感影像的混合象元问题, 如Landsat的MSS卫星影像单个象元对应地表79米*79米的矩形区域, 影像上记录的光谱数据是每个象元所对应的地表区域内所有地物类型的光谱辐射的总和效果。 因而,这种误差不仅有形态上的畸形,还可能包括属性方面的偏差。
7.2.2. 决定栅格单元代码的方式 #
在决定栅格代码时尽量保持地表的真实性,保证最大的信息容量。 图7-5所示的一块矩形地表区域,内部含有A、B、C三种地物类型,O点为中心点, 将这个矩形区域近似地表示为栅格结构中的一个栅格单元时,可根据需要, 采取如下的方式之一来决定栅格单元的代码。 图 7.5 栅格单元代码的确定 # 用处于栅格中心处的地物类型或现象特性决定栅格代码,在图7-5所示的矩形区域中, 中心点O落在代码为C的地物范围内,按中心点法的规则,该矩形区域相应的栅格单元代码为C, 中心点法常用于具有连续分布特性的地理要素,如降雨量分布、人口密度图等。 以占矩形区域面积最大的地物类型或现象特性决定栅格单元的代码,在图7-5所示的例子中, 显见B类地物所占面积最大,故相应栅格代码定为B。 面积占优法常用于分类较细,地物类别斑块较小的情况。 根据栅格内不同地物的重要性,选取最重要的地物类型决定相应的栅格单元代码, 假设图7-5中A类最重要的地物类型,即A比B和C类更为重要,则栅格单元的代码应为A。 重要性法常用于具有特殊意义而面积较小的地理要素,特别是点、线状地理要素, 如城镇、交通枢纽、交通线、河流水系等,在栅格中代码应尽量表示这些重要地物。 根据矩形区域内各地理要素所占面积的百分比数确定栅格单元的代码,如可记面积最大的两类BA, 也可以根据B类和A类所占面积百分比数在代码中加入数字。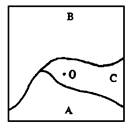
中心点法 #
面积占优法 #
重要性法 #
百分比法 #
7.2.3. 编码方法 #
直接栅格编码 #
这是最简单直观而又非常重要的一种栅格结构编码方法,通常称这种编码的图像文件为网格文件或栅格文件, 栅格结构不论采用何种压缩编码方法,其逻辑原型都是直接编码网格文件。 直接编码就是将栅格数据看作一个数据矩阵,逐行(或逐列)逐个记录代码,可以每行都从左到右逐个象元记录, 也可以奇数行地从左到右而偶数行地从右向左记录,为了特定目的还可采用其他特殊的顺序(图7-6)。 图 7.6 一些常用的栅格排列顺序 # 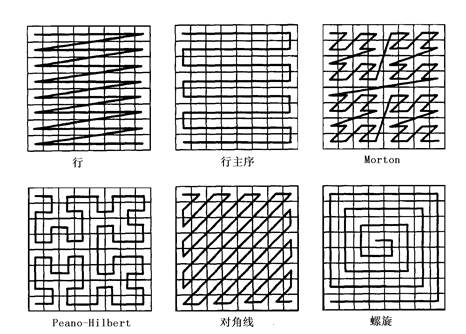
压缩编码方法 #
目前有一系列栅格数据压缩编码方法,如键码、游程长度编码、块码和四叉树编码等。 其目的,就是用尽可能少的数据量记录尽可能多的信息,其类型又有信息无损编码和信息有损编码之分。 信息无损编码是指编码过程中没有任何信息损失,通过解码操作可以完全恢复原来的信息, 信息有损编码是指为了提高编码效率,最大限度地压缩数据,在压缩过程中损失一部分相对不太重要的信息, 解码时这部分难以恢复。 在地理信息系统中多采用信息无损编码,而对原始遥感影像进行压缩编码时,有时也采取有损压缩编码方法。
1)链码(Chain Codes)
链码又称为弗里曼链码[Freeman]或边界链码,链码可以有效地压缩栅格数据, 而且对于估算面积、长度、转折方向的凹凸度等运算十分方便,比较适合于存储图形数据。 缺点是对边界进行合并和插入等修改编辑工作比较困难,对局部的修改将改变整体结构,效率较低, 而且由于链码以每个区域为单位存储边界,相邻区域的边界将被重复存储而产生冗余。
2)游程长度编码(Run-Length Codes)
游程长度编码是栅格数据压缩的重要编码方法,它的基本思路是: 对于一幅栅格图像,常常有行(或列)方向上相邻的若干点具有相同的属性代码, 因而可采取某种方法压缩那些重复的记录内容。 其方法有两种方案: 一种编码方案是,只在各行(或列)数据的代码发生变化时依次记录该代码以及相同的代码重复的个数, 从而实现数据的压缩。 例如对图7-4(c)所示栅格数据,可沿行方向进行如下游程长度编码:
(0,1),(4,2),(7,5);(4,5),(7,3);(4,4),(8,2),(7,2);(0,2),(4,1),(8,3),(7,2);(0,2),(8,4),(7,1),(8,1);(0,3),(8,5);(0,4),(8,4);(0,5),(8,3)。
只用了44个整数就可以表示,而在前述的直接编码中却须要64个整数表示, 可见游程长度编码压缩数据是十分有效又简便的。 事实上,压缩比的大小是与图的复杂程度成反比的,在变化多的部分,游程数就多,变化少的部分游程数就少, 图件越简单,压缩效率就越高。 另一种游程长度编码方案就是逐个记录各行(或列)代码发生变化的位置和相应代码, 如对图7-4(c)所示栅格数据的另一种游程长度编码如下(沿列方向):
(1,0),(2,4),(4,0),(1,4),(4,0);(1,4),(5,8),(6,0);(1,7),(2,4),(4,8),(7,0);(1,7),(2,4),(3,8),(8,0);(1,7),(3,8);(1,7),(6,8);(1,7),(5,8)。
游程长度编码在栅格压缩时,数据量没有明显增加,压缩效率较高,且易于检索,叠加合并等操作,运算简单, 适用于机器存储容量小,数据需大量压缩,而又要避免复杂的编码解码运算增加处理和操作时间的情况。
3)块码
块码是游程长度编码扩展到二维的情况,采用方形区域作为记录单元,每个记录单元包括相邻的若干栅格, 数据结构由初始位置(行、列号)和半径,再加上记录单位的代码组成。 对图7-4(c)所示图像的块码编码如下:
(1,1,1,0),(1,2,2,4),(1,4,1,7),(1,5,1,7),
(1,6,2,7),(1,8,1,7),(2,1,1,4),(2,4,1,4),
(2,5,1,4),(2,8,1,7),(3,1,1,4),(3,2,1,4),
(3,3,1,4),(3,4,1,4),(3,5,2,8),(3,7,2,7),
(4,1,2,0),(4,3,1,4),(4,4,1,8),(5,3,1,8),
(5,4,2,8),(5,6,1,8),(5,7,1,7),(5,8,1,8),
(6,1,3,0),(6,6,3,8),(7,4,1,0),(7,5,1,8),
(8,4,1,0),(8,5,1,0)。
该例中块码用了120个整数,比直接编码还多,这是因为例中为描述方便,栅格划分很粗糙,在实际应用中, 栅格划分细,数据冗余多的多,才能显出压缩编码的效果,而且还可以作一些技术处理, 如行号可以通过行间标记而省去记录,行号和半径等也不必用双字节整数来记录,可进一步减少数据冗余。
块码具有可变的分辨率,即当代码变化小时图块大,就是说在区域图斑内部分辨率低; 反之,分辨率高以小块记录区域边界地段,以此达到压缩的目的。 因此块码与游程长度编码相似,随着图形复杂程度的提高而降低效率,就是说图斑越大,压缩比越高; 图斑越碎,压缩比越低。 块码在合并、插入、检查延伸性、计算面积等操作时有明显的优越性。 然而在某些操作时,则必须把游程长度编码和块码解码,转换为基本栅格结构进行。
4)四叉树
四叉树又称四元树或四分树,是最有效的栅格数据压缩编码方法之一, 绝大部分图形操作和运算都可以直接在四叉树结构上实现,因此四叉树编码既压缩了数据量, 又可大大提高图形操作的效率。 四叉树将整个图像区逐步分解为一系列被单一类型区域内含的方形区域,最小的方形区域为一个栅格象元, 分割的原则是,将图像区域划分为四个大小相同的象限, 而每个象限又可根据一定规则判断是否继续等分为次一层的四个象限,其终止判据是,不管是哪一层上的象限, 只要划分到仅代表一种地物或符合既定要求的少数几种地物时,则不再继续划分, 否则一直划分到单个栅格象元为止。 四叉树通过树状结构记录这种划分,并通过这种四叉树状结构实现查询、修改、量算等操作。 图7-7(b)为图7-4(c)图形的四叉树分解,各子象限尺度大小不完全一样,但都是同代码栅格单元, 其四叉树如图7-7-(c)所示。 图 7.7 块码分割; 四叉树分割 # 图 7.8 b的四叉树编码 # 四叉树编码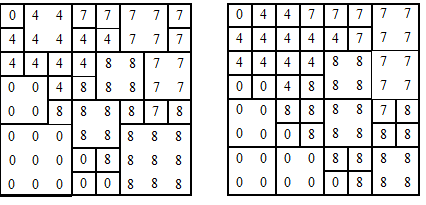
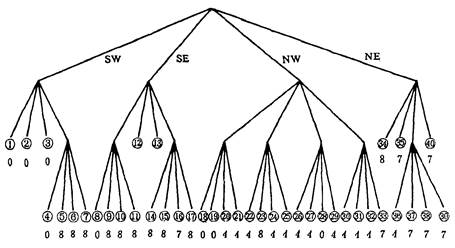
其中最上面的那个结点叫做根结点,它对应整个图形。 总共有4层结点,每个结点对应一个象限,如2层4个结点分别对应于整个图形的四个象限, 排列次序依次为南西(SW)、南东(SE)、北西(NW)和北东(NE), 不能再分的结点称为终止结点(又称叶子结点),可能落在不同的层上,该结点代表的子象限具有单一的代码, 所有终止结点所代表的方形区域覆盖了整个图形。 从上到下,从左到右为叶子结点编号如图7-7(c)所示,共有40个叶子结点, 也就是原图被划分为40个大小不等的方形子区,图7-7(c)的最下面的一排数字表示各子区的代码。
由上面图形的四叉树分解可见,四叉树中象限的尺寸是大小不一的,位于较高层次的象限较大,深度小即分解次数少, 而低层次上的象限较小,深度大即分解次数多, 这反映了图上某些位置单一地物分布较广而另一些位置上的地物比较复杂,变化较大。 正是由于四叉树编码能够自动地依照图形变化而调整象限尺寸,因此它具有极高的压缩效率。
采用四叉树编码时,为了保证四叉树分解能不断地进行下去, 要求图像必须为2 n ×2 n 的栅格阵列,n为极限分割数, n+1为四叉树的最大高度或最大层数, 图7-4(c)为2 3 ×2 3 的栅格,因此最多划分三次, 最大层数为4, 对于非标准尺寸的图像需首先通过增加背景的方法将图像扩充为2 n ×2 n 的图像。
为了使计算机既能以最小的冗余存储图像对应的四叉树,又能方便地完成各种图形图像操作, 专家们已提出了多种编码方式,下面介绍美国马里兰大学地理信息系统中采用的编码方式, 该方法记录了终止结点(或叶子结点)的地址和值,值就是子区的代码,其中地址包括两个部分, 共32位(二进制),最右边4位记录该叶子结点的深度,即处于四叉树的第几层上, 有了深度可以推知子区的大小;地址由从根结点到该叶子结点的路径表示,0,1,2, 3分别表示SW、SE、NW、NE,从右边第5位开始2n字节记录这些方向。 如图7-7-(c)表示的第六个结点深度为3,第一层处于SW象限,记为0; 第二层处于NE象限,记为3,第三层处于NW象限,记为2,表示为二进制为:
0000… 000(22位);001110(6位);0011(4位)
每层象限位置由两位二进制数表示,共6位,十进制整数为227。 这样,记录了各个叶子的地址,再记上相应代码值,就记录了这个图像,并可在此编码基础上进行多种图像操作。
事实上,叶结点的地址可以直接由子区左下角的行列坐标,按二进制按位交错得到。 如对于6号叶子结点,在以图像左下角为原点的行列坐标系中,其左下角行、列坐标为(3,2), 表示为二进制分别为011和010,按位交错就是001110,正是6号地块。
对于只有点状地物或只有线状地物的图件,为了提高效率,设计了略有不同的划分终止条件和记录方法, 称为点四叉树和线四叉树。 点四叉树对子象限的划分直到每个子象限不含有点或只含有一个点为止, 叶子的值则记录是否有点和点在子象限的位置;线四叉树划分子象限直到子象限不含线段或只含有单个线段, 对线的结点则划分到单个象素,其叶子值记录更为复杂。
四叉树编码具有可变的分辨率,并且有区域性质,压缩数据灵活,许多运算可以在编码数据上直接实现, 大大地提高了运算效率,是优秀的栅格压缩编码之一。
一般说来,对数据的压缩是以增加运算时间为代价的。 在这里时间与空间是一对矛盾,为了更有效地利用空间资源,减少数据冗余,不得不花费更多的运算时间进行编码, 好的压缩编码方法就是要在尽可能减少运算时间的基础上达到最大的数据压缩效率,并且是算法适应性强, 易于实现。 链码的压缩效率较高,已经近矢量结构,对边界的运算比较方便,但不具有区域的性质,区域运算困难; 游程长度编码既可以在很大程度上压缩数据,又最大限度地保留了原始栅格结构,编码解码十分容易; 块码和四叉树码具有区域性质,又具有可变的分辨率,有较高的压缩效率, 四叉树编码可以直接进行大量图形图像运算,效率较高,是很有前途的方法。 在此基础上已经开始发展了用于三维数据的八叉树编码等。