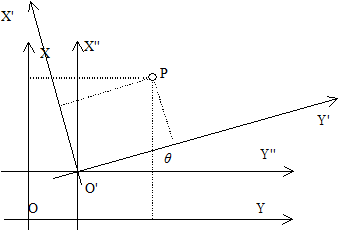
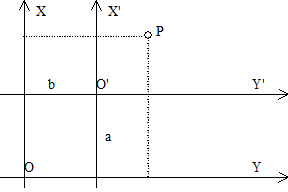
所谓坐标系,包含两方面的内容:一是在把大地水准面上的测量成果化算到椭球体面上的计算工作中, 所采用的椭球的大小; 二是椭球体与大地水准面的相关位置不同,对同一点的地理坐标所计算的结果将有不同的值。 因此,选定了一个一定大小的椭球体,并确定了它与大地水准面的相关位置,就确定了一个坐标系(图4-3)。 图 4.3 现实世界和坐标空间的联系 # 地球除了绕太阳公转外,还绕着自己的轴线旋转,地球自转轴线与地球椭球体的短轴相重合,并与地面相交于两点, 这两点就是地球的两极,北极和南极。 垂直于地轴,并通过地心的平面叫赤道平面,赤道平面与地球表面相交的大圆圈(交线)叫赤道。 平行于赤道的各个圆圈叫纬圈(纬线)(Parallel),显然赤道是最大的一个纬圈。 通过地轴垂直于赤道面的平面叫做经面或子午圈(Meridian),所有的子午圈长度彼此都相等。 (图4-4) 图 4.4 地球的经线和纬线 # 设椭球面上有一点P(图4-4),通过P点作椭球面的垂线,称之为过P点的法线。 法线与赤道面的交角,叫做P点的地理纬度(简称纬度),通常以字母 φ 表示。 纬度从赤道起算,在赤道上纬度为0度,纬线离赤道愈远,纬度愈大,至极点纬度为90度。 赤道以北叫北纬、以南叫南纬。 过P点的子午面与通过英国格林尼治天文台的子午面所夹的二面角,叫做P点的地理经度(简称经度), 通常用字母λ表示。 国际规定通过英国格林尼治天文台的子午线为本初子午线(或叫首子午线),作为计算经度的起点, 该线的经度为0度,向东0-180度叫东经,向西0-180度叫西经。 地面上任一点的位置,通常用经度和纬度来决定。 经线和纬线是地球表面上两组正交(相交为90度)的曲线,这两组正交的曲线构成的坐标,称为地理坐标系。 地表面某两点经度值之差称为经差,某两点纬度值之差称为纬差。 例如北京在地球上的位置可由北纬39°56'和东经116°24'来确定。 地理坐标是一种球面坐标。 由于地球表面是不可展开的曲面,也就是说曲面上的各点不能直接表示在平面上,因此必须运用地图投影的方法, 建立地球表面和平面上点的函数关系,使地球表面上任一点由地理坐标 (φ、λ) 确定的点, 在平面上必有一个与它相对应的点,平面上任一点的位置可以用极坐标或直角坐标表示。 在平面上选一点 O 为直角坐标原点, 过该点 O 作相互垂直的两轴 X’OX 和 Y’OY 而建立平面直角坐标系, 如图5所示。 直角坐标系中,规定 OX、OY 方向为正值, OX、OY 方向为负值, 因此在坐标系中的一个已知点 P , 它的位置便可由该点对 OX 与 OY 轴的垂线长度唯一地确定,即 x=AP , y=BP ,通常记为 P(x,y) 。 图 4.5 平面直角坐标系和极坐标系 # 如图5所示,设 O’ 为极坐标原点, O’O 为极轴, P 是坐标系中的一个点, 则 O’P 称为极距,用符号 ρ 表示,即 ρ=O’P 。 ∠OO’P 为极角,用符号 δ 表示,则 ∠OO’P=δ 。 极角 δ 由极轴起算,按逆时针方向为正,顺时针方向为负。 极坐标与平面直角坐标之间可建立一定的关系式。 由图5可知,直角坐标的x轴与极轴重合,二坐标系原点间距离 OO’ 用 Q 表示,则有: X=Q–ρcosδ Y=ρsinδ 如图4-6所示,坐标系 XOY 与坐标系 X’O’Y’ 相应的坐标轴彼此平行, 并且具有相同的正向。 坐标系 X’O’Y’ 是由坐标系 XOY 平行移动而得到的。 设 P 点在坐标系 XOY 中的坐标为 (x,y) , 在 X’O’Y’ 中坐标为 (x’,y’) ,而 (a, b) 是 O’ 在坐标系 XOY 中的坐标,于是: x=x’+a y=y’+b 上式即一点在坐标系平移前后之坐标关系式。 图 4.6 坐标平移 # 如图4-7所示,如坐标系 XOY 与坐标系 X’O’Y’ 的原点重合, 且对应的两坐标轴夹角为 θ , 坐标系 X’O’Y’ 是由坐标系 XOY 以O为中心逆时针旋转 θ 角后得到的。 x=x’cosθ+y’sinθ y=y’cosθ-x’sinθ 上式即为经过旋转θ角后的二直角坐标系中某一点坐标的关系式。 图 4.7 坐标旋转 # 如图4-8所示,坐标系 X’O’Y’ 的原点在坐标系 XOY 中的坐标为a、b, X 轴与 X’ 轴之夹角为θ。 可以认为坐标系 X’O’Y’ 原是与坐标系XOY重合,后因为O’分别平移了a、b之距离, 并且坐标系二坐标轴 O’X’ 与 O’Y’ 又相对 OX 与 OY 逆时针旋转了 θ 角而得到的。 在二坐标系之间引入一个辅助坐标系 X”O’Y” , 使它的二坐标轴 O’X” 与 O’Y” 分别与 OX 、 OY 平行。 在 X”O’Y” 系中有一点P,其坐标为 (x”,y”) , 则由坐标系平移公式与坐标系旋转公式可得: x=x”+a y=y”+b 故有 x”=x’cosθ+y’sinθ y”=y’cosθ-x’sinθ 即 x=x’cosθ+y’sinθ+a y”=y’cosθ-x’sinθ+b 上式即坐标系平移和旋转后新、旧坐标系中某一点坐标之关系式。 图 4.8 坐标平移和旋转 # 
4.2.1. 地理坐标 #
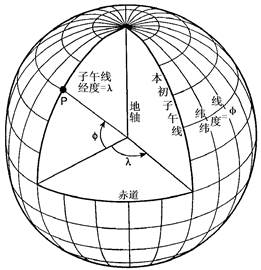
纬度(Latitude) #
经度(Longitude) #
地面上点位的确定 #
4.2.2. 平面上的坐标系 #
平面直角坐标系的建立 #
平面极坐标系(Polar Coordinate)的建立 #

4.2.3. 直角坐标系的平移和旋转 #
坐标系平移 #
坐标系旋转 #
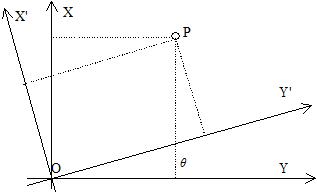
坐标系平移和旋转 #