4.1. 地球椭球体基本要素

地球的形状 #

为了从数学上定义地球，必须建立一个地球表面的几何模型。 这个模型由地球的形状决定的。 它是一个较为接近地球形状的几何模型，即椭球体，是由一个椭圆绕着其短轴旋转而成。

地球自然表面是一个起伏不平、十分不规则的表面，有高山、丘陵和平原，又有江河湖海。 地球表面约有71%的面积为海洋所占用，29%的面积是大陆与岛屿。 陆地上最高点与海洋中最深处相差近20公里。 这个高低不平的表面无法用数学公式表达，也无法进行运算。 所以在量测与制图时，必须找一个规则的曲面来代替地球的自然表面。 当海洋静止时，它的自由水面必定与该面上各点的重力方向（铅垂线方向）成正交，我们把这个面叫做水准面。 但水准面有无数多个，其中有一个与静止的平均海水面相重合。 可以设想这个静止的平均海水面穿过大陆和岛屿形成一个闭合的曲面，这就是大地水准面（图4-1）。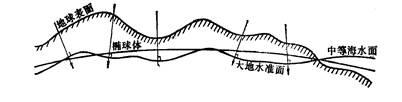

大地水准面所包围的形体，叫大地球体。 由于地球体内部质量分布的不均匀，引起重力方向的变化， 导致处处和重力方向成正交的大地水准面成为一个不规则的，仍然是不能用数学表达的曲面。 大地水准面形状虽然十分复杂，但从整体来看，起伏是微小的。 它是一个很接近于绕自转轴（短轴）旋转的椭球体。 所以在测量和制图中就用旋转椭球来代替大地球体，这个旋转球体通常称地球椭球体，简称椭球体。

地球的大小 #

关于地球椭球体的大小，由于采用不同的资料推算，椭球体的元素值是不同的。 现将世界各国常用的地球椭球体的数据列表如下：

表4-1：各种地球椭球体模型

椭球体的半径 #

地球椭球体表面是一个规则的数学表面。 椭球体的大小，通常用两个半径：长半径a和短半径b，或由一个半径和扁率来决定。 扁率 α 表示椭球的扁平程度。 扁率的计算公式为： α=（a-b）/a 。 这些地球椭球体的基本元素 a、b、α 等，由于推求它的年代、使用的方法以及测定的地区不同， 其结果并不一致，故地球椭球体的参数值有很多种。

中国在1952年以前采用海福特（Hayford）椭球体， 从1953-1980年采用 克拉索夫斯基 椭球体。 随着人造地球卫星的发射，有了更精密的测算地球形体的条件。 1975年第16届国际大地测量及地球物理联合会上通过国际大地测量协会第一号决议中公布的地球椭球体，称为GRS（1975），中国自1980年开始采用GRS（1975）新参考椭球体系。 由于地球椭球长半径与短半径的差值很小，所以当制作小比例尺地图时，往往把它当作球体看待， 这个球体的半径为6371公里。

高程 #

地面点到大地水准面的高程，称为绝对高程。 如图2所示， P:sub:`0`P:sub:`0`' 为大地水准面， 地面点 A 和 B 到 P:sub:`0`P:sub:`0`' 的垂直距离 H:sub:`A` 和 H:sub:`B` 为 A、B 两点的绝对高程。 地面点到任一水准面的高程，称为相对高程。 如图2中， A、B 两点至任一水准面 P:sub:`1`P:sub:`1`' 的垂直距离 H:sub:`A`' 和 H:sub:`B`' 为 A、B 两点的相对高程。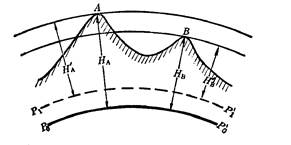

我国的大地控制网

我国面积辽阔，在约960万平方公里的土地上进行测图工作，需要分成若干单元测区， 而且测量的精度又要符合统一要求，为此，在全国范围内建立统一的大地控制网。 控制网分为平面控制网和高程控制网。

大地坐标： 在地面上建立一系列相连接的三角形，量取一段精确的距离作为起算边，在这个边的两端点， 采用天文观测的方法确定其点位（经度、纬度和方位角），用精密测角仪器测定各三角形的角值， 根据起算边的边长和点位，就可以推算出其他各点的坐标。 这样推算出的坐标，称为大地坐标。

我国1954年在北京设立了大地坐标原点，由此计算出来的各大地控制点的坐标，称为1954年北京坐标系。 我国1986年宣布在陕西省泾阳县设立了新的大地坐标原点， 并采用1975年国际大地测量协会推荐的大地参考椭球体，由此计算出来的各大地控制点坐标， 称为1980年大地坐标系。

我国高程的起算面是黄海平均海水面。 1956年在青岛设立了水准原点，其他各控制点的绝对高程都是根据青岛水准原点推算的，称此为1956年黄海高程系。 1987年国家测绘局公布：中国的高程基准面启用《1985国家高程基准》取代国务院1959年批准启用的《黄海平均海水面》。 《1985国家高程基准》比《黄海平均海水面》上升29毫米。

比例尺表示法 #

地图比例尺通常认为是地图上距离与地面上相应距离之比。 地图比例尺可用下述方法表示。

1）数字比例尺

这是简单的分数或比例，可表示为1：1000000或1/1000000，最好用前者。 这意味着，地图上（沿特定线）长度1毫米、1厘米或1英寸（分子）， 代表地球表面上的1000000毫米、厘米或英寸（分母）。

2）文字比例尺

这是图上距离与实地距离之间关系的描述。 例如，1：1000000这一数字比例尺可描述为“图1毫米等于实地1公里”。

3）图解比例尺或直线比例尺

这是在地图上绘出的直线段，常常绘于图例方框中或图廓下方，表示图上长度相当于实地距离的单位。

面积比例尺

这关系到图上面积与实地面积之比，表示图上1单位面积（平方厘米）与实地上同一种平方单位的特定数量之比。

比例系数 #

表明确定的比例尺与实际比例尺数值之间的关系叫做比例系数（SF）。 可以这样理解比例系数，首先将地球缩小为所选比例尺的地球仪地图；然后将该球形地图转换为平面地图。 上述平面地图的数字比例尺就是地球仪的比例尺，叫做主比例尺（或名义比例尺）； 真实比例尺就是平面地图上的实际比例尺，当然各处是不相同的。

比例系数可按下式计算：SF=实际比例尺/主比例尺

该公式表明，比例系数是实际比例尺与单位（1）主比例尺之比。 当比例系数为2时，实际比例尺为主比例尺的两倍。 比例系数只在小比例尺世界地图上比较明显。 在大比例尺地图上，各处的比例系数对于1只有很小的变化。