3.4.1. 空间关系的基本概念 #
在地理信息系统中集中存储了以下的内容:
空间分布位置信息
属性信息
拓扑空间关系信息。
由此可见,空间位置、关系与度量的描述在GIS中起着举足轻重的作用。
地理要素之间的空间区位关系可抽象为点、线(或弧)、多边形(区域)之间的空间几何关系,其关系如下, 如图3-12示。 图 3.12 地理要素之间的部分拓扑空间关系 # 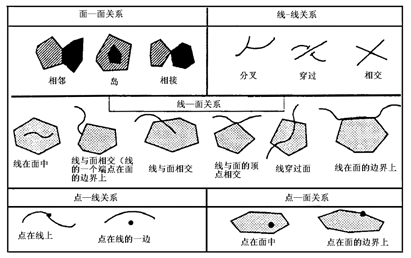
1)点——点关系
相合;
分离;
一点为其它诸点的几何中心;
一点为其它诸点的地理重心。
2)点——线关系
点在线上:可以计算点的性质,如拐点等;
线的端点:起点和终点;
线的交点;
点与线分离:可计算点到线的距离。
3)点——面关系
点在区域内,可以记数和统计;
点为区域的几何中心;
点为区域的地理重心;
点在区域的边界上;
点在区域外部。
4)线——线关系
重合;
相接:首尾环接或顺序相接;
相交:
相切;
并行。
5)线——面关系
区域包含线:可计算区域内线的密度;
线穿过区域:
线环绕区域:对于区域边界,可以搜索其左右区域名称;
线与区域分离。
6)面——面关系
包含:如岛的情形;
相合:
相交:可以划分子区,并计算逻辑与、或、非和异或;
相邻:计算相邻边界的性质和长度;
分离:计算距离、引力等。
近年来,空间关系的理论与应用研究在国内外都非常多。 究其原因,一方面是它为地理信息系统数据库的有效建立、空间查询、空间分析、辅助决策等提供了最基本的关系; 另一方面是将空间关系理论应用于地理信息系统查询语言,形成一个标准的SQL空间查询语言, 可以通过API(Application Program Interface,应用程序接口)进行空间特征的存储、提取、查询、更新等。
空间关系包含三种基本类型,即拓扑关系、方向关系、度量关系。
3.4.2. 拓扑空间关系分析 #
拓扑属性 #
拓扑一词来自于希腊文,意思是“形状的研究”。 拓扑学是几何学的一个分支,它研究在拓扑变换下能够保持不变的几何属性——拓扑属性。 为了得到一些拓扑的感性认识,假设欧氏平面是一张高质量无边界的橡皮, 该橡皮能够伸长和缩短到任何理想的程度。 想象一下基于这张橡皮所绘制的图形,允许这张纸伸长但是不能撕破或者重叠,这样原来图形的一些属性将保留, 而有些属性将会失去。 例如,在橡皮表面有一个多边形,多边形内部有一个点。 无论对橡皮进行压缩或拉伸,点依然存在于多边形内部,点和多边形之间的空间位置关系不改变, 而多边形的面积则会发生变化。 前者则是空间的拓扑属性,后者则不是拓扑属性。 表3-2列出了包含在欧氏平面中的对象的拓扑和非拓扑属性。
表3-2:欧氏平面上实体对象所具有的拓扑和非拓扑属性
拓扑属性 | 一个点在一个弧段的端点 一个弧段是一个简单弧段(弧段自身不相交) 一个点在一个区域的边界上 一个点在一个区域的内部 一个点在一个区域的外部 一个点在一个环的内部 一个面是一个简单面(面上没有“岛”) 一个面的连续性(给定面上任意两点,从一点可以完全在面的内部沿任意路径走向另一点) |
非拓扑属性 | 两点之间的距离 一个点指向另一个点的方向 弧段的长度 一个区域的周长 一个区域的面积 |
从表中可以看出,拓扑属性描述了两个对象之间的关系, 因此又称为拓扑关系(TopologicalRelation)。 图3-13为拓扑空间关系的形式化表达。 图 3.13 拓扑空间中的点和邻域 # 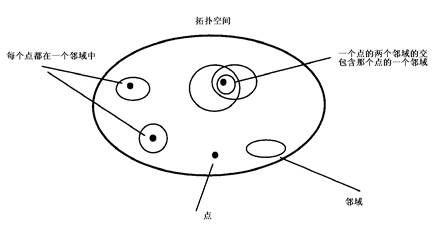
拓扑描述的数学基础——点集拓扑学 #
拓扑学是几何学分支之一,作为近代数学的一门基础理论学科, 拓扑学已经渗透到数学的许多分支以及物理、化学和生物学之中,而且在工程技术中也获得了广泛的应用。 由于拓扑学是研究图形在拓扑变化下不变的性质,拓扑学已成为地理信息系统空间关系的理论基础, 为空间点、线、面之间的包含、覆盖、相离和相接等空间关系的描述提供直接的理论依据。
- 定义1
\(X\) 为一非空集合, \(\rho : X\times X \rightarrow R\) 为一映射, 如果对于任意的 \(x,y,z \in X\) ,有:
\(\rho(x,y)\ge 0\) ,并且 \(\rho(x,y)=0\) , iff \(x=y\) ;
\(\rho(x,y)=\rho(y,x)\) ;
\(\rho(x,z) \le \rho(x,y) + \rho(y,z)\) (三角不等式);
则称 ρ 为 X 的度量,偶对 (X,ρ) 称为度量空间。
- 定义2 :
A 为度量空间 X 的子集,如果 A 的每一点都有一个球形邻域包含于 A ,则称 A* 为 ρ 的开集。
定义3 : X 为非空集合, A 为 X 的子集族,如果满足下列条件:
X 和空集 Φ 属于 A ;
(2)若*A1,A2*属于 A ,则 A1与A2 的交集属于 A ;
(3)*A*中任意两个元素的并仍为A中的元素;
则称 A 为 X 的拓扑。 如果 A 为集合 X 的拓扑,则称偶对 (X,A) 为拓扑空间。
定义4 : A 为拓扑空间 X 的子集。如果点 x 属于 X 的每一邻域 U 中都有 A 中异于 x 的点,即 U∩(A~{x})≠Φ ,则称 x 为 A 的聚点或极限点。 A 的聚点可以属于 A 也可以不属于 A 。
定义5: A 为拓扑空间 X 的子集,集合A的所有聚点构成的集合称为A的导集,记作dX(A)或d(A)。
定义6: A 为拓扑空间 X 的子集,如果 A 的每一聚点都属于 A ,即 d(A) 为 A 的子集,则称 A 为闭集。
定义7: X 为拓扑空间, X 的子集 A 与 A 的导集 d(A) 的并集 A∪d(A) 称为 A 的闭包,记作 C(A) 。
定义8: 为拓扑空间 X 的子集,如果 A 是点 x 属于 X 的邻域,即存在 X 的开集 U 使得 x 属于 U , U 为 A 的子集,则称点 x 为集合 A 的内点。集合 A 的所有内点构成的集合,称为A的内部,记作 I(A) 。
定义9: A 为拓扑空间 X 的子集,对于点 x 属于 X ,如果在 x 的任一邻域 U 中既有 A 的点又有 ~A 的点,即: U∩A≠Φ 并且 U∩(~A)≠Φ ,则称 x 为集合 A 的边界点。集合 A 的所有边界点的集合称为集合 A 的边界,记作 B(A) 。
定理1: A为拓扑空间X的任意子集,则:
C(A)=~I(~A)=I(A)∪B(A)
I(A)=~C(~A)=C(A)~B(A)
B(A)=C(A)∩C(~A)=~(I(A)∪I(~A))=B(~A)
拓扑空间关系描述——9交模型 #
设有现实世界中的两个简单实体A、B,B(A)、B(B)表示A、B的边界, I(A)、I(B)表示A、B的内部,E(A)、E(B)表示A、B余。 Egenhofer[1993]构造出一个由边界、内部、余的点集组成的9-交空间关系模型(9-IntersectionModel,9-IM)如下:
B(A)∩B(B) | B(A)∩I(B) | B(A)∩E(B) |
I(A)∩B(B) | I(A)∩I(B) | I(A)∩E(B) |
E(A)∩B(B) | E(A)∩I(B) | E(A)∩E(B) |
对于该矩阵中的每一元素,都有“空”与“非空”两种取值, 9个元素总共可产生2 9 =512种情形。
9交模型形式化地描述了离散空间对象的拓扑关系,基于9交模型,可以定义空间数据库的一致性原则,并应用于数据库更新、维护中。此外,9交模型也是进一步研究空间关系的基础。
9交模型一共可以表达512种可能的空间关系,但是在实际上,有些关系并不存在。表2给出了面/面(A/A),面/线(A/L),面/点(A/P),线/线(L/L),线/点(L/P),点/点(P/P)可能空间关系的矩阵形式。其中“-”表示不可能存在该关系,“Yb”表示在单值和多值的矢量图上都可能存在的关系,“Ym”在多值的矢量图上可能存在的关系。
表3-3: 通过9-交模型表示的两个要素可能的拓扑关系(表中将矩阵的9个数值展开得到一个二进制数值, 1表示相应交集不为空,0表示交集为空)
关系 | 9-交模型矩阵 | A/A | A/L | A/P | L/L | L/P | P/P |
|---|---|---|---|---|---|---|---|
r026 | 000011010 | Yb | |||||
r030 | 000011110 | Yb | Yb | ||||
r031 | 000011111 | Yb | Yb | Yb | |||
r063 | 000111111 | Yb | Yb | ||||
r092 | 001011100 | Yb | Yb | ||||
r093 | 001011101 | Yb | |||||
r095 | 001011111 | Yb | |||||
r127 | 001111111 | Yb | |||||
r159 | 010011111 | Yb | |||||
r179 | 010110011 | Ym | Ym | ||||
r191 | 010111111 | Yb | Yb | ||||
r220 | 011011100 | Ym | Yb | Ym | |||
r223 | 011011111 | Yb | |||||
r252 | 011111100 | Yb | |||||
r253 | 011111101 | Yb | |||||
r255 | 011111111 | Yb | Ym | ||||
r272 | 100010000 | Ym | |||||
r277 | 100010101 | Yb | |||||
r279 | 100010111 | Yb | |||||
r284 | 100011100 | Yb | Yb | ||||
r285 | 100011101 | Yb | Yb | ||||
r287 | 100011111 | Yb | Yb | Yb | |||
r311 | 100110111 | Yb | |||||
r316 | 100111100 | Yb | |||||
r317 | 100111101 | Yb | |||||
r319 | 100111111 | Yb | |||||
r349 | 101011101 | Yb | |||||
r373 | 101110101 | Yb | |||||
r400 | 110010000 | Ym | Ym | ||||
r412 | 110011100 | Yb | |||||
r415 | 110011111 | Yb | |||||
r435 | 110110011 | Ym | Ym | ||||
r439 | 110110111 | Yb | |||||
r444 | 110111100 | Yb | |||||
r445 | 110111101 | Yb | |||||
r447 | 110111111 | Yb | |||||
r476 | 111011100 | Ym | Yb | Ym | |||
r477 | 111011101 | Yb | |||||
r501 | 111110101 | Yb | |||||
r508 | 111111100 | Yb | |||||
r509 | 111111101 | Yb | |||||
r511 | 111111111 | Yb |
从上表可以看出,可能的拓扑关系数目要远远少于512个(面/面: 6,面/线: 19,面/点: 3,线/线: 16,线/点: 3,点/点: 2)。 图3-14给出了这些可能关系的图示。 从某种意义上讲,9-交模型所描述的拓扑关系只是拓扑关系的类别,对于每一类别可以有多种可能的情形, 例如两条相交的线,一个交点的情形和多个交点的9-交模型表示是一致的,但是其拓扑关系并不同。 图 3.14 9-交模型所述拓扑关系图示 # 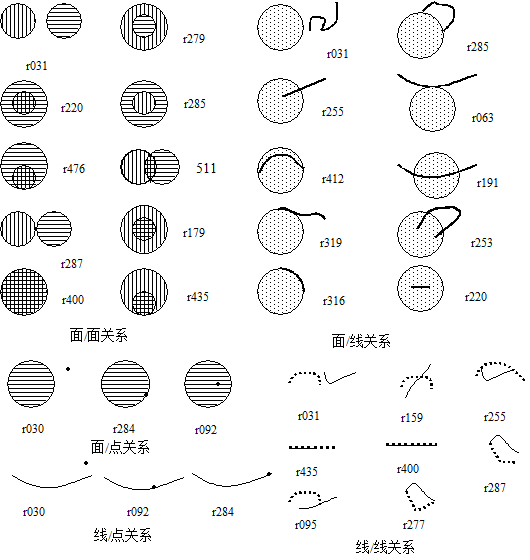
9交模型的扩展
通过引进点集的余,9-交空间关系模型增强了面/线、线/线空间关系的唯一性。 但它仅仅用“空”与“非空”来区分两个目标的边界、内部、余, 对面/面、点/点、点/线、点/面的空间关系描述并无多大改进。 为此,该方法仍有一定的局限性。
在地理信息系统中,数据可以划分为几何数据与属性数据两大类型。 由于几何数据具有可量测性,为此地理信息系统所涉及的客观世界是一个度量空间, 而且每个度量空间又是一个拓扑空间。 根据目标的自由度,基本实体可划分为点、线、面三种基本类型。 点状目标具有固定的位置和方向,将其定义为零维目标; 线状目标都有一条有形或无形的定位线,将其定义为一维目标; 面状目标都有一个有形或无形的轮廓线,将其定义为二维目标。
运用维数扩展法,将9-IM进行扩展, 利用点、线、面的边界、内部、余之间的交集的维数来作为空间关系描述的框架。 对于几何实体的边界,它是比其更低一维的几何实体的集合。 为此,点的边界为空集; 线的边界为线的两个端点,当线为闭曲线时,线的边界为空;面的边界由构成面的所有线构成。 若设P为一个点集,定义点集的求维函数DIM如下:
利用维数扩展法,9交模型可扩展为
DIM(B(A)∩B(B)) | DIM(B(A)∩I(B)) | DIM(B(A)∩E(B)) |
DIM(I(A)∩B(B)) | DIM(I(A)∩I(B)) | DIM(I(A)∩E(B)) |
DIM(E(A)∩B(B)) | DIM(E(A)∩I(B)) | DIM(E(A)∩E(B)) |
根据DE-9IM,对于点集拓扑空间X,当需要进行关系判别时,可对矩阵的9元取值进行分析、比较。 令C为各单元交的点集,其取值P可能为 {T,F,*,0,1,2} 。 各个取值的具体含义为:
P=T DIM(C)∈{0,1,2},即交集C包含有点、线、面;P=F DIM(C)=-1,即交集C为空;P= DIM(C)∈{-1,0,1,2},即两目标交集既有点、线、面,又含有某些部分的交为空的情形,该情况在关系判别时,一般不予以考虑;P=0 DIM(C)=0;P=1 DIM(C)=1;P=2 DIM(C)=2。
扩展9-交模型中各元素通过取值
{T,F,\*,0,1,2}
, 可产生的情形为
6^9
=10077696
种,关系非常复杂, 通过对大量的空间关系进行归纳和分类,得出5种基本的空间关系: 相离关系(Disjoint)、相接关系(Touch)、相交关系(Cross)、包含于关系(In)、交叠关系(Overlap), 并将这5种关系定义为空间关系的最小集,其特征为:
相互之间不能进行转化;
能覆盖所有的空间关系模式;
能应用于同维与不同维的几何目标;
每一种关系对应于唯一的DE-9IM矩阵;
任何其它的DE-9IM关系可以通过用这5种基本关系进行表达。
拓扑空间关系识别 #
在地理信息系统中,空间数据具有属性特征、空间特征和时间特征, 基本数据类型包括属性数据、几何数据和空间关系数据。 作为基本数据类型的空间关系数据主要指点/点、点/线、点/面、线/线、线/面、面/面之间的相互关系。
3.4.3. 方向空间关系分析 #
方向关系描述 #
方向关系又称为方位关系、延伸关系,它定义了地物对象之间的方位, 如“河北省在河南省北部”就描述了方向关系。 为了定义空间目标之间的方向关系,首先定义点目标之间的关系。 给定定位参考,即相互垂直的X、Y坐标轴,方向关系的定义采用垂直于坐标轴的直线为参考。 令 P:sub:`i` 为目标 P 的点( P 为原目标), Q:sub:`j` 为目标 Q 的点( Q 为参考目标), X(P:sub:`i`) 与 Y(P:sub:`i`) 函数返回点 P:sub:`i` 的X、Y坐标。 则 P 与 Q 在二维空间中具有以下8种可能关系,并提供了一个完整的关系覆盖。 这些关系定义为:
Restricted_East(P:sub:`i`,Q:sub:`j`)= X(P:sub:`i`)>X(Q:sub:`j`) And Y(P:sub:`i`)=Y(Q:sub:`j`)
Restricted_South(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)=X(Q:sub:`j`) And Y(P:sub:`i`)<Y(Q:sub:`j`)
Restricted_West(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)<X(Q:sub:`j`) And Y(P:sub:`i`)=Y(Q:sub:`j`)
Restricted_North(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)=X(Q:sub:`j`) And Y(P:sub:`i`)>Y(Q:sub:`j`)
North_West(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)<X(Q:sub:`j`) And Y(P:sub:`i`)>Y(Q:sub:`j`)
North_East(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)>X(Q:sub:`j`) And Y(P:sub:`i`)>Y(Q:sub:`j`)
South_West(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)<X(Q:sub:`j`) And Y(P:sub:`i`)<Y(Q:sub:`j`)
South_East(P:sub:`i`,Q:sub:`j`)=X(P:sub:`i`)>X(Q:sub:`j`) And Y(P:sub:`i`)<Y(Q:sub:`j`)
以上8种关系通过点的投影可以精确判断。 如有任意两点,上述8种关系必有一种满足。 而且,这些关系具有传递性,另外一些关系可进行相互转换(如North_East(PI, QJ)South_West(QI,PJ),通过对上述8种关系进行扩充,可得出另外4种方向关系,即:
East(P:sub:`i`,Q:sub:`j`)=North_East(P:sub:`i`,Q:sub:`j`)Or Restricted_East(P:sub:`i`,Q:sub:`j`) OrSouth_East(P:sub:`i`,Q:sub:`j`)
South(P:sub:`i`,Q:sub:`j`)=South_West(P:sub:`i`,Q:sub:`j`)Or Restricted_South(P:sub:`i`,Q:sub:`j`) OrSouth_East(P:sub:`i`,Q:sub:`j`)
West(P:sub:`i`,Q:sub:`j`)=North_West(P:sub:`i`,Q:sub:`j`)Or Restricted_West(P:sub:`i`,Q:sub:`j`) OrSouth_West(P:sub:`i`,Q:sub:`j`)
North(P:sub:`i`,Q:sub:`j`)=North_West(P:sub:`i`,Q:sub:`j`)Or Restricted_North(P:sub:`i`,Q:sub:`j`) OrNorth_East(P:sub:`i`,Q:sub:`j`)
以点目标之间的方向关系为基础,其余目标之间的方向关系可类似定义。
方向关系识别 #
MBR(Minimum BoundingRectangle)指的是空间目标的外切矩形。 MBR的表示非常简单,只需利用两点(左上、右下角点)表示即可。 由于MBR的简单、实用性,MBR广泛应用于空间目标数据结构表示以及空间数据查询中。
为了确定目标之间是否具有某种方向关系,首先可判断目标之间的MBR是否具有该关系, 然后再利用点/点关系进一步进行关系判断,确定具体的关系。
3.4.4. 度量空间关系分析 #
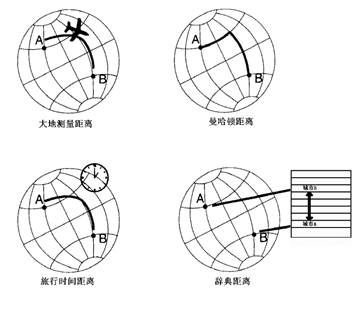
基本空间对象度量关系包含点/点、点/线、点/面、线/线、线/面、面/面之间的距离。 在基本目标之间关系的基础上,可构造出点群、线群、面群之间的度量关系。 例如,在已知点/线拓扑关系与点/点度量关系的基础上,可求出点/点间的最短路径、最优路径、服务范围等; 已知点、线、面度量关系,进行距离量算、邻近分析、聚类分析、缓冲区分析、 泰森多边形 分析等。 定量量测区域空间指标和区域地理景观间的空间关系是地理信息系统特有的能力。 其中区域空间指标包括: 几何指标:位置、长度(距离)、面积、体积、形状、方位等指标; 自然地理参数:坡度、坡向、地表辐照度、地形起伏度、河网密度、切割程度、通达性等; 人文地理指标:如集中指标、区位商、差异指数、地理关联系数、吸引范围、交通便利程度、人口密度等。 地理空间中两点间的距离度量可以沿着实际的地球表面进行,也可以沿着地球椭球体的距离量算,具体的, 距离可以表现为以下几种形式(以地球上两个城市之间的距离为例)(图3-15): 大地测量距离 :该距离即沿着地球大圆经过两个城市中心的距离。 曼哈顿距离 :纬度差加上经度差(名字“曼哈顿距离”是由于在曼哈顿,街道的格局可以被模拟成两个垂直方向的直线的一个集合)。 旅行时间距离 :从一个城市到另一个城市的最短的时间可以用一系列指定的航线来表示(假设每个城市至少有一个飞机场)。 词典编纂距离 :在一个固定的地名册中一系列城市中它们位置之间的绝对差值。 图 3.15 地球上各种形式的距离 # 空间指标量算 #
地理空间的距离度量 #